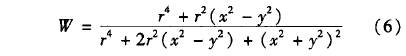摘要:采用有限元方法,针对三对多电极电磁流量计电极在不同位置时权重函数分布情况进行数值仿真。提出2个描述权重函数分布均匀度的指标:最大偏差和整体均匀度,并在电极数目和位置不同情况下对权重函数的分布情况进行分析比较。结果表明,电磁流量计权重函数分布不仅与电极数目有关,还与电极所在的位置有关。通过合理设计电极位置,三对电极电磁流量计在权重函数分布均匀度和平均强度两方面都优于单电极对电磁流量计。.
1引言
电磁流量计是一种用于导电性液体流量测量的仪表o由于其不受温度、压力、流体密度和粘度等因素影响,且其内部光滑无阻流部件[3],不会对流体产生阻力从而导致压力损失,因此在工业生产过程的流量测量中得到广泛应用。权重函数表示管道横截面上不同位置流速对流量计输出信号的贡献大小,权重函数均匀则各点流速贡献相同。所以,在电磁流量计的设计中,总是希望权重函数分布越均匀越好。对外流式电磁流量计和油管之间环形区域的权重函数分布情况进行了理论推导和仿真。管道横截面上流体速度呈非轴对称分布时,采用传统单电极对电磁流量计会产生较大的测量误差。而多电极电磁流量计可以从多角度多位置测量感应电动势,故可用于非轴对称管流流量的精确测量。
目前,对多电极电磁流量计权重函数分布情况的还较少。本文多电极电磁流量计在管道横截面上权重函数的分布特性。结果可为多电极电磁流量计传感器的结构优化提供进--步的基础。
2基本方程与权重函数
当导电性液体在磁场中作切割磁力线运动时,液体中有感应电流产生。根据欧姆定律有:

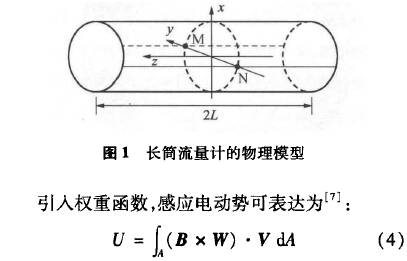
对均匀磁场型电磁流量计,为便于分析和阐明其物理意义,通常使用“长筒流量计”物理模型[13]如图1所示,设磁场区域长度和电极长度均为2L,此时电极呈线状。当L-→∞时,方程的求解就可由三维空间坐标问题简化成=维平面坐标问题。
式中:A为测量管容积,W为权重函数,W=▽G,G为格林函数。W是三维空间函数,Wx、Wy、Ws分别为W在坐标轴x、y、z方向,上分量,对长简流量计只考虑y方向上分量Wy。假设磁场方向平行于x轴,流速平行于z轴,则B=Bx,V=Vz。由以上条件,可得:
(B×W)·V=BWyV(5)
由式(5)可知,电极两端产生的感应电动势不仅与流速有关,还与权重函数分布有关。
3权重函数的仿真与分析
3.1单电极对电磁流量计权重函数数值仿真
根据格林函数性质和电磁流量计边界条件,可得长筒流量计权重函数解析式[7]:
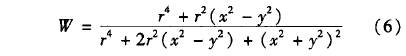
式中r为管道内半径。由式(6)可得管道内电极所在横截面上W的分布情况,r=1时其等值线分布如图2所示。
由图2可知,在管道中心处W值为1,沿着y轴.向电极M、N处移动时,W值逐渐增大;沿着x轴向管壁移动时,W值逐渐减小至0.5。权重函数越大的区域内的流体速度对电极M、N所产生感应电动势的贡献越大。由权重函数分布规律可以看出,整个测量区域内的流体速度对电极所产生感应电动势的影响程度不一样,这就解释了传统单电极对电磁流量计对流速分布的敏感性,导致其无法准确测得非轴对称流的平均流速。
采用有限元方法,使用Malab软件中PDE工具.箱,对单电极对电磁流量计在管道内电极所在横截面上权重函数分布情况进行数值仿真。在数值仿真时,关键是求解格林函数G,由于C满足拉普拉斯方程▽2G=0,假设电磁流量计边界条件如下:

(4)对求解区域网格化,网格划分越细,精度越高,但计算量会增大;
(5)求解椭圆型偏微分方程可得u,即G;
(6)求解格林函数G在y方向上的梯度,即Wy;
(7)画出Wy的等值线分布图。
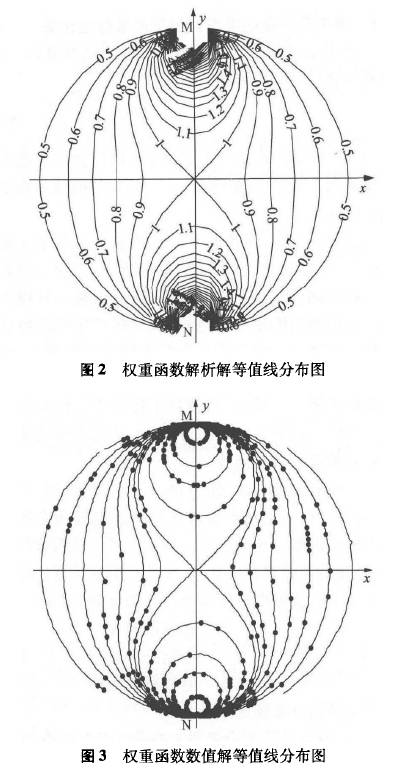
如图3所示,为权重函数数值解等值线。将其与图2进行对比,发现二者没有太大差别。表明利用有限元方法计算权重函数是高效可行的方法,并且可通过增加网格密度来提高计算精度。
3.2三对电极电磁流量计权重函数数值仿真
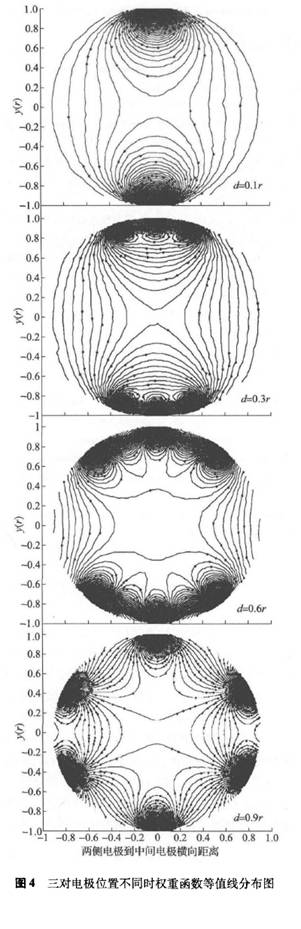
针对三对电极电磁流量计,对电极处于管道横截面上不同位置时权重函数的分布情况分别进行仿真,结果如图4所示。三对电极的位置分布如下:中间一对电极横坐标为x=0,两侧电极关于中间电极对称,它们到中间电极的横向距离为d,d的范围为0.1r~0.9r,其中r为传感器管道内半径。
3.3权重函数的数值分析
定义:对管道横截面上权重函数分布进行数值仿真时,设求解区域被划分成n个网格,第k个网格对应的权重函数值为Wk(k=1,2,.,n),则权重函数W的最大偏差RM可表示为:RM=MAX

应区域内权重函数的最大偏差程度;RD则反应了区域内权重函数分布的整体均匀程度,RD值越小,权重函数分布的整体均匀程度越理想。
依据上面两个指标,计算电极处于不同位置时权重函数分布均匀度,如表1所示。从图4和表1可知,权重函数分布情况不仅与电极数目有关,还与电极分布的位置有关;随着两侧电极与中间电极距离增大,权重函数的平均值W0逐渐减小,即相同流速对流量计输出信号的贡献逐渐减弱;随着两侧电极与中间电极距离增大,权重函数的最大偏差Rm和RD的值都逐渐增大,权重函数的整体均匀度逐渐降低。
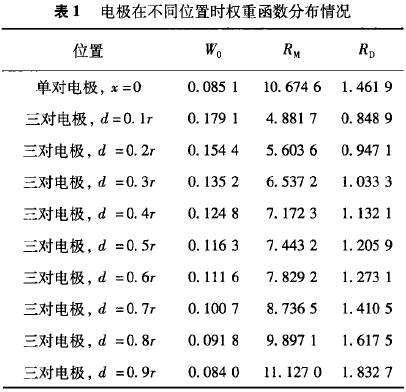
权重函数均匀度Rp随电极位置变化趋势如图5所示。从表1和图5可知,对于三对电极电磁流量计,当中间一对电极横坐标为x=0,两侧电极到中间电极的横向距离d≤0.7r时,整体均匀度Rp<1.4619,最大偏差RM<10.6746,即三对电极电磁流量计比传统单电极对电磁流量计权重函数分布的更为均匀,其管道横截面.上不同位置流体速度对流量计输出信号的贡献更趋向-致,表明三对电极电磁流量计对流速分布的敏感性减弱;权重函数平均值W0>0.0851,表明相比单电极对电磁流量计,管道横截面上相同流速对流量计输出信号的贡献增强,即在相同条件下,三对电极电磁流量计可获得更强的感应电动势信号。
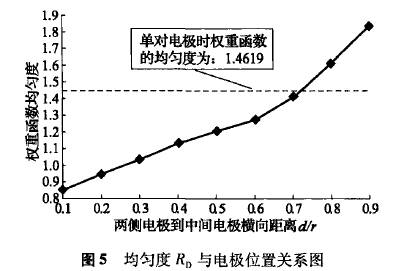
以上针对三对电极电磁流量计权重函数分布随电极位置变化情况进行了仿真分析,结果为多电极电磁流量计的结构优化提供了参考依据,具有-定的理论指导意义。虽然从理论上电极数目越多,流体平均速度的测量精度越高,但从实际制作、成本和可靠性来讲,电极数目不可能无限增多,而且电极数目的增加会延长数据采集时间,导致系统实时性降低,通常只要测量精度达到要求就可以了。当然对精度有特殊要求时,可相应增加或减少电极数目。
4结论
采用有限元方法对传统单电极对电磁流量计权重函数分布进行了数值仿真,将仿真结果与已有权重函数解析解作对比分析,验证了有限元方法求解权重函数的可行性和有效性;针对三对电极电磁流量计,电极在不同位置时,对电极所在横截面上权重函数分布情况分别进行数值仿真;定义了两个描述权重函数分布均匀度的指标:最大偏差和整体均匀度。依据这两个指标,在电极数目和位置不同情况下,分别对权重函数进行仿真分析。结果表明通过合理设计电极位置,三电极对电磁流量计在权重函数分布均匀度和平均强度两方面都优于单电极对电磁流量计。
以上内容源于网络,如有侵权联系即删除!